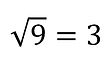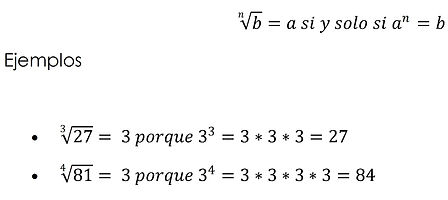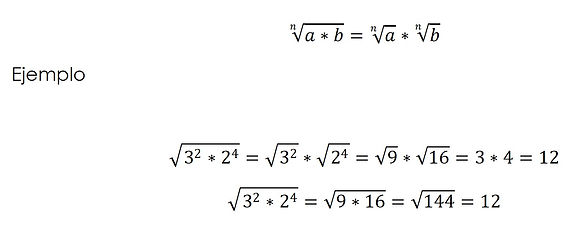-
Concepto
La radicación es la operación inversa de la potenciación.
Llamamos raíz n-ésima de un número dado a al número b que elevado a n nos da a.
En la radicación se distinguen los siguientes términos:
-
Radicando: Es el número al que se calcula su raíz.
-
Índice: Es el número que indica la raíz que se extrae. Cuando el índice es 2, no es necesario escribirlo.
-
Raíz: es el resultado de efectuar la operación.
-
Radical: es el símbolo de raíz.
La radicación es la operación que “deshace” la potenciación
En el ejemplo anterior, el 9 se llama radicando, el 2 índice y el resultado 3, raíz.
La definición formal de esta operación es la siguiente:
Si n es un número natural, se dice que el número entero a es la raíz enésima del número entero b, si b es la potencia enésima de a. Es decir:
Veamos que sucede cuando el radicando es un numero negativo
2. Propiedades de la radicación
La radicación es en realidad otra forma de expresar una potenciación: la raíz de cierto orden de un número es equivalente a elevar dicho número a la potencia inversa. Por esto, las propiedades de la potenciación se cumplen también con la radicación. Para que estas propiedades se cumplan, se exige que el radicando de las raíces sea positivo.
Raíz de un producto
La raíz de un producto es igual al producto de las raíces de los factores:
Raíz de cociente
La raíz de una fracción es igual al cociente de la raíz del numerador entre la raíz del denominador:
Raíz de una raíz
Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva el radicando
Ejemplo