FASE 2
Dominar el método para hallar el máximo común divisor
Introducción
El máximo común divisor de varios números es el mayor de sus divisores comunes
-
Definición y Ejemplo
El máximo común divisor de dos números a y b es el número más grande que divide a a y divide a b.
Para denotar el máximo común divisor de a y b escribiremos
M.C.D.(a, b) ó MCD(a, b).
Ejemplo: Vamos a calcular el máximo común divisor de 12 y 18.
Puesto que el número que buscamos tiene que dividir a 12 y a 18, no puede ser mayor que 12.
En la siguiente tabla escribimos los candidatos:
Divisor de 12?
1 - si
2 - si
3 - si
4 - si
5 - no
6 - si
7 - no
8 - no
9 - no
10 - no
11 - no
12 - si
Divisor de 18?
1 - si
2 - si
3 - si
4 - no
5 - no
6 - si
7 - no
8 - no
9 - si
10 - no
11 - no
12 - no
Puesto que el máximo común divisor debe dividir a los dos números, las únicas posibilidades son: 1, 2, 3 y 6.
Como tiene que ser el más grande posible, el MCD es 6.
M.C.D. (12, 18)=6
2. Descomposición en Números Primos
Vamos a recordar cómo descomponer números para escribirlos como un producto de números primos, lo cual facilitará el cálculo del máximo común divisor
Podemos escribir cualquier número como producto de potencias de números primos
Ejemplo
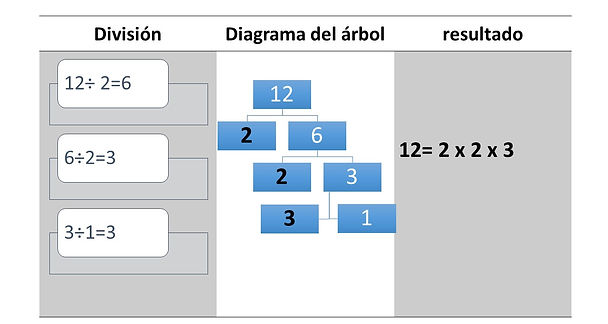
Para descomponer un número dividimos el número sucesivamente entre números primos hasta llegar a 1.
Ejemplo:
Dividimos sucesivamente por números primos (de modo que la división sea exacta).
La descomposición es el producto de las potencias de los números primos cuyos exponentes indican el número de veces que hemos dividido por dicho primo.
En la descomposición tenemos que escribir una potencia de base 2 y una potencia de base
3.
Los exponentes son el número de veces que se repite el número:
-
El 2 se repite 2 veces.
-
El 3 se repite 4 veces.
Por tanto, la descomposición de 324 es
324=3^4 *2^2
3. Obtención del MCD a partir de las descomposiciones
Regla para el MCD: «comunes al menor exponente»
La forma más rápida de calcular el máximo común divisor de dos números es:
-
Descomponemos los números en números primos (producto de potencias de primos).
-
El máximo común divisor es el producto de las potencias que aparecen en las dos descomposiciones,
-
pero cuyo exponente sea el menor.
Ejemplo:
Calculamos el máximo común divisor de 180 y 324.
Sus descomposiciones son:
180=2^2 * 3^2 *5
324=3^4 *2^2
El máximo común divisor será el producto de una potencia de base 2 y otra de base 3, ya que son las bases que aparecen en las dos descomposiciones.
-
la potencia de base 2 tiene el exponente 2 en las dos descomposiciones, así que escribiremos
2^2
-
la potencia de base 3 tiene los exponentes 2 y 4. Nos quedamos con el menor:
3^2
Por tanto, el máximo común divisor de 180 y 324 es
MCD (180, 324)
= 22 * 32
= 4*9
= 36
4.El MCD de más de dos números
Podemos calcular el máximo común divisor de más de dos números.
Para ello usaremos el mismo criterio: «comunes al menor exponente».
Ejemplo:
Calculamos el M.C.D. de 60, 90 y 150.
Las descomposiciones de estos números son:
60= 2^2 *3*5
90=2*3^2*5
150= 3*2*5^2
Las bases de las potencias son: 2, 3 y 5. Y todas son bases comunes.
-
El menor exponente de la base 2 es 1.
-
El menor exponente de la base 3 es 1.
-
El menor exponente de la base 5 es 1.
-
Por tanto, el MCD es M.C.D. (60, 90, 150)
= 2*3*5
= 30