FASE 1
Dominar el método para hallar el mínimo común múltiplo
Objetivo: Comprender cuales son los números primos y compuestos y resolver problemas de la vida cotidiana donde se requiere implementación del mínimo común múltiplo
Introducción
Un número natural es divisor de otro, si lo divide exactamente

Los múltiplos de un número natural son los resultados de
multiplicar ese número por todos los números naturales
-
Definición y Ejemplo
El mínimo común múltiplo de dos números a y b es el número más pequeño que es múltiplo de a y múltiplo de b.
Para denotar el mínimo común múltiplo de a y b escribiremos m.c.m. (a, b) o mcm(a, b).
Ejemplo:
Vamos a calcular el mínimo común múltiplo de 4 y 6. Para ello, escribimos los primeros múltiplos de 4 y de 6:
Recuerda que los múltiplos se obtienen multiplicando. Entre los 9 primeros múltiplos de 4 y de 6, los múltiplos 12, 24 y 36 son múltiplos de ambos (son múltiplos comunes).
Tenemos que quedarnos con el mínimo.
Por tanto, el mínimo común múltiplo de 4 y 6 es 12:
m.c.m (4,6)=12
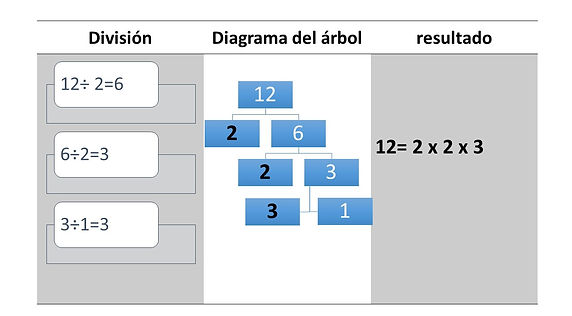
2. Descomposición en números primos
Recordamos como descomponer números para escribirlos como un producto de números primos, lo cual facilitara el cálculo del mínimo común múltiplo.
Podemos escribir cualquier número como producto de potencias de números primos. Por ejemplo,
Para descomponer un número dividimos el número sucesivamente entre números primos hasta llegar a 1.
La descomposición es el producto de las potencias de los números primos, siendo sus exponentes el número de veces que hemos dividido por dicho primo.
Ejemplo:
En la descomposición tenemos que escribir una potencia de base 2 y un numero de base 31.
Los exponentes son el número de veces que se repite el numero:
-
El 2 se repite 3 veces.
-
El 31 no se repite.
Por tanto, la descomposición de 324 es
248= 2^3 x 31
3.Obtención del MCM
Regla para calcular el mcm:
«Bases comunes y no comunes al mayor exponente»
Método:
-
Descomponemos los números en números primos (producto de potencias de primos).
-
El mínimo común múltiplo es el producto de todas las potencias que aparecen en las descomposiciones, pero si alguna de las bases aparece en ambas descomposiciones, escogemos la de mayor exponente.
Ejemplo:
Calculamos el mínimo común múltiplo de 180 y 324.
Sus descomposiciones son:
180= 2^2 * 3^2 *5
324= 3^4 * 2^2
El mínimo común múltiplo tendrá las potencias de base 5, de base 3 y de base 2.
-
la potencia de base 2 tiene el exponente 2 en las dos descomposiciones, así que escribiremos 22
-
la potencia de base 3 tiene los exponentes 2 y 4. Nos quedamos con el mayor: 34
-
la potencia de base 5 silos aparece en una de las descomposiciones, pero este hecho es irrelevante.
Por tanto, el mínimo común múltiplo de 180 y 324 es
MC.M (180, 324)
=2^2 * 3^4 *5
=1620
El procedimiento anterior puede resumirse como comunes y no comunes al mayor exponente, lo que significa que el mcm es el producto de todas las potencias que aparecen en una o en ambas descomposiciones («comunes y no comunes») pero cuyo exponente sea el mayor.
También, podemos calcular el mínimo común múltiplo de más de dos números. Para ello, usamos la misma regla: comunes y no comunes al mayor exponente.
Ejemplo
Calculamos el m.c.m. de 8, 9 y 10.
Las descomposiciones de estos números son:
8= 2^3
9= 3^2
10= 2*5
Las bases de las potencias son: 2, 3 y 5.
El mayor exponente para la base 2 es 3.
Las otras dos bases solo tienen un exponente posible.
Por tanto, el mcm(8,9,10) es
M.C.M. (8, 9, 10)=
=2^3 * 3^2 *5
=8*9*5
= 360